ロケットの設計において最も重要な方程式にロケット方程式というものがあります。
今回はロケット方程式の導出を行います。
Point
ロケット方程式は以下の3つの式で表される。
$$v=c\ln \left(\frac{m_{0}}{m_{t}}\right)\tag{1.1}$$
$$v_{f}=c\ln \left(\frac{1}{\mathrm{MR}}\right)\tag{1.2}$$
$$v_{f}=g_{0}I_{sp}\ln \left(\frac{1}{\mathrm{MR}}\right)\tag{1.3}$$
ロケット方程式の導出①(運動量保存則のみ使用)
運動量保存則を示してロケット方程式を導出します。
まず図1のような任意の時刻\(Δt\)で,一定の質量で推進薬を消費する状況を考えます。
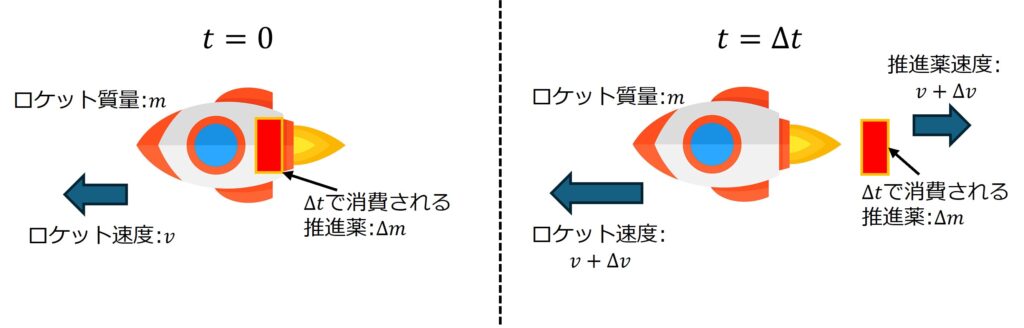
\(t=0\)と\(t=Δt\)における運動量保存則を用いると以下のような式を示すことができます。
式(2.1)を計算すると以下のようになります。
$$mΔv=cΔm\tag{2.2}$$
式(2.2)を微分方程式の形で表すために,以下のような変形をします。
$$Δv=\frac{dv}{dt}Δt\tag{2.3}$$
$$Δm=-\frac{dm}{dt}Δt\tag{2.4}$$
式(2.4)について,質量\(m\)は減少し,かつ\(Δm\)は正の値をとるためマイナスをかける必要があります。
式(2.3)と式(2.4)を式(2.2)に代入し,\(Δt\)を両辺から打ち消すと以下のような式となります。
$$dv=-\frac{c}{m}dm\tag{2.5}$$
これで微分方程式の形になりました。ここから変数分離形を用いて式(2.5)を解きます。
式(2.5)の両辺を0から任意の時間\(t\)まで積分すると以下のような式になります。
$$\displaystyle \int_{0}^{t} dv=-c\displaystyle \int_{0}^{t} \frac{1}{m} dm\tag{2.6}$$
式(2.6)を計算すると以下のようになります。計算過程を知りたい方はこちらをご覧ください。
$$v=c\ln \left(\frac{m_{0}}{m_{t}}\right)\tag{2.7}$$
これがロケット方程式となります。\(m_{t}\)は任意の時刻\(t\)でのロケットの質量を表します。
また,燃焼時間を\(t_{b}\)として,\(t=t_{b}\)とすると燃焼終了後のロケットの速度\(v_{f}\)は以下のようになります。
$$v_{f}=c\ln \left(\frac{1}{\mathrm{MR}}\right)\tag{2.8}$$
\(\mathrm{MR}\)はマスレシオ(Mass Ratio)の略で,日本語だと質量比という意味になります。
質量比は以下のような式で表されます。
$$\mathrm{MR}=\frac{m_{f}}{m_{0}}\tag{2.9}$$
\(m_{0}\)は全備質量で燃料を消費していないときのロケットの初期質量を指します。
\(m_{f}\)は空虚質量で燃料を消費し終わったときのロケットの空の質量となります。
式(2.8)もロケット方程式となります。式(2.7)は任意の時刻\(t\)におけるロケット方程式で,式(2.8)は燃焼終了時\(t_{b}\)でのロケット方程式となります。
ロケット方程式の導出②(検査面を使用)
ロケット方程式の導出は上記の①を理解すれば十分ですが,さらに理解を深めたい人は当項目もご覧ください。
有効排気速度に関する記事で,検査面を使用して推力の原理の式を示しました。
検査面から,推力\(F\)の式を表すと以下のようになります。(詳しくはこちらの記事をご覧ください。)
$$F=\dot{m}c\tag{3.1}$$
\(\dot{m}\)が燃料の質量流量,\(c\)が有効排気速度です。
また,ニュートンの第二法則より推力\(F\)は式(3.2)のように表すこともできます。
$$F=\frac{d}{dt}mv\tag{3.2}$$
式(3.2)は運動方程式における物体にはたらく力\(F\)は運動量を微分したものという意味を表しています。今回は,物体にはたらく力\(F\)が推力となります。
式(3.1)と式(3.2)より,以下のように表されます。
$$dv=\frac{F}{m}dt=\frac{c\dot{m}}{m}dt\tag{3.3}$$
式(3.3)を変数分離形で時刻0から燃焼終了の\(t_{b}\)まで積分すると,燃焼終了後のロケットの速度\(v_{f}\)は以下のようになります。
計算過程を見たい方はこちらをご覧ください。
$$v_{f}=c\ln \left(\frac{1}{\mathrm{MR}}\right)\tag{3.4}$$
また,有効排気速度\(c\)は比推力\(I_{sp}\)と標準重力加速度\(g_{0}\)を用いて表すと以下のようになります。式(3.5)の導出はこちらの記事をご覧ください。
$$c=g_{0}I_{sp}\tag{3.5}$$
よって,式(3.4)と式(3.5)より以下のようになります。
$$v_{f}=g_{0}I_{sp}\ln \left(\frac{1}{\mathrm{MR}}\right)\tag{3.6}$$
ロケット方程式の活用
最後に,ロケット方程式がロケットやミサイルの設計の上でどのように活用されるのか解説します。
そもそもロケットとは,ペイロードを運ぶための乗り物です。
ロケットならば人工衛星・人・補給物資を運び,ミサイルならば弾頭を運びます。
ペイロードをロケットエンジンによって十分に加速させ,目的地に届けるのがロケットの役割です。
そこでロケット方程式が重要になります。
ロケットエンジンによって出せる速度が大きいほどより大きな質量のペイロードを運べることが可能となり,より遠くに飛ばすことができます。
ロケットやミサイルは全備質量のうち,90%以上がペイロードを加速させるためのエンジンの燃料です。詳しくはこちらの記事をご覧ください。
ロケットやミサイルの設計において,ロケットが出せる速度をロケット方程式によって算出することが重要となります。
また,式(3.5)よりロケット方程式は比推力\(I_{sp}\)と質量比\(\mathrm{MR}\)のみによって燃焼終了後の速度が決まります。
ロケットの速度は比推力と質量比というたった2つの指標によって決定されるということがロケット方程式から分かります。
とてもシンプルですね。
比推力\(I_{sp}\)は温度や大気圧によっても変わりますが,主には燃料の種類によって決定されます。
比推力が大きい燃料であるほどロケットはより速度を得ることができます。
日本の国産ロケットであるH-ⅡA/Bロケット,H3ロケットの燃料と酸化剤が液体水素/液体酸素を使用する理由は比推力が450sと大きいからです。
また,質量比もダイレクトに速度に効いてきます。
質量比が小さいほどより対数の真数部分が大きくなりますからロケットが軽いほど速度が出ることが分かります。
質量比を小さくするには多くの燃料を積み,できるだけ空虚重量を軽くすることが重要です。
ロケットの燃焼終了後の速度は比推力と質量比によってのみ決まりますから,燃料の消費の仕方を変えても理論上は最終的に出せる速度は変わりません。
しかし,空気抵抗や重力の影響を考慮すると燃料の燃やし方によっても速度は変わります。
このロケット方程式は空気抵抗と重力の影響を考慮していないということには注意しましょう。
参考文献
- ロケットエンジン,中村佳朗 監修/鈴木弘一 著



コメント