ロケットのパラメータにおいて有効排気速度というものがあります。
有効排気速度はロケット方程式にも登場する重要なパラメータです。
そこで有効排気速度の意味と式の導出を解説します。
Point
- 有効排気速度はロケットの速度に圧力推力を加えた値である。
- 有効排気速度は以下の式で表すことができる。
$$c=v_{2}+\frac{(p_{2}-p_{3})A_{2}}{\dot{m_{2}}}$$
\(v_{2}\):排気速度
\(p_{2}\):ノズル面の圧力
\(p_{3}\):検査面3の外気圧
\(\dot{m_{2}}\):燃料の質量流量
有効排気速度の式の導出
有効排気速度は式を見れば意味が理解できるので,式の導出をしたあとに意味を解説します。
まずは以下の図のような状況を考えます。
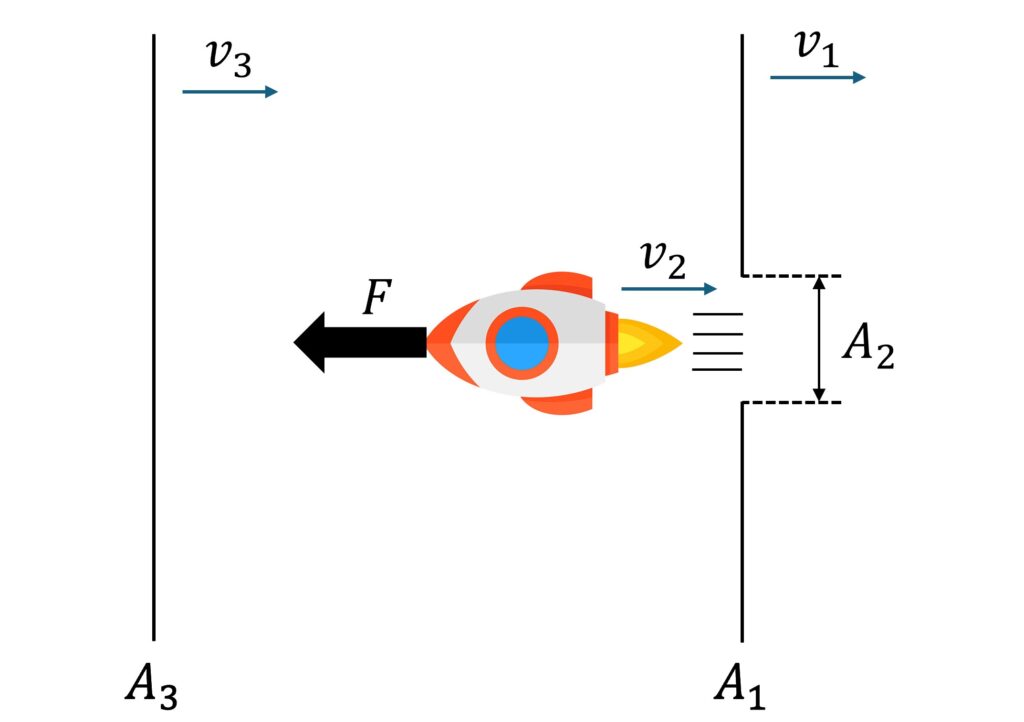
定常流(圧力・速度・密度が一定の流れ)の中をロケットが一定の推力\(F\)で進み,検査面\(A_{1}\)と\(A_{3}\)を設定します。
また,ロケットのノズルの出口面積を\(A_{2}\)とします。
このような状況からロケットの推力\(F\)を計算してみます。
力学の復習をすると「力\(F\)は運動量\(M\)を微分したもの」です。つまり,式(1)のように表すことができます。
$$F=\frac{dM}{dt}\tag{1}$$
流体の運動量変化によって得られたロケットの推力を運動量推力と呼びます。
また,検査面\(A_{1}\)と\(A_{3}\)ではロケットが検査面\(A_{3}\)を通過したことにより検査面が受ける圧力が変化しています。
この変化した圧力もロケットの推力\(F\)に加わります。この推力のことを圧力推力\(F_{p}\)と呼びます。
以上のことからロケットの推力\(F\)は式(2)のように計算することができます。
$$F=\frac{dM}{dt}+F_{p}=\left(\frac{M_{3}-M_{1}}{Δt}\right)+F_{p}$$
$$=\frac{(m_{3}v_{3}+m_{2}v_{2})-m_{1}v_{1}}{Δt}+[p_{3}(A_{3}-A_{2})+p_{2}A_{2}]-p_{1}A_{1}$$
$$=(\dot{m_{3}}v_{3}+\dot{m_{2}}v_{2})-\dot{m_{1}}v_{1}+[p_{3}(A_{3}-A_{2})+p_{2}A_{2}]-p_{1}A_{1}\tag{2}$$
ここで,式(2)の各項が何を指しているのか確認しましょう。
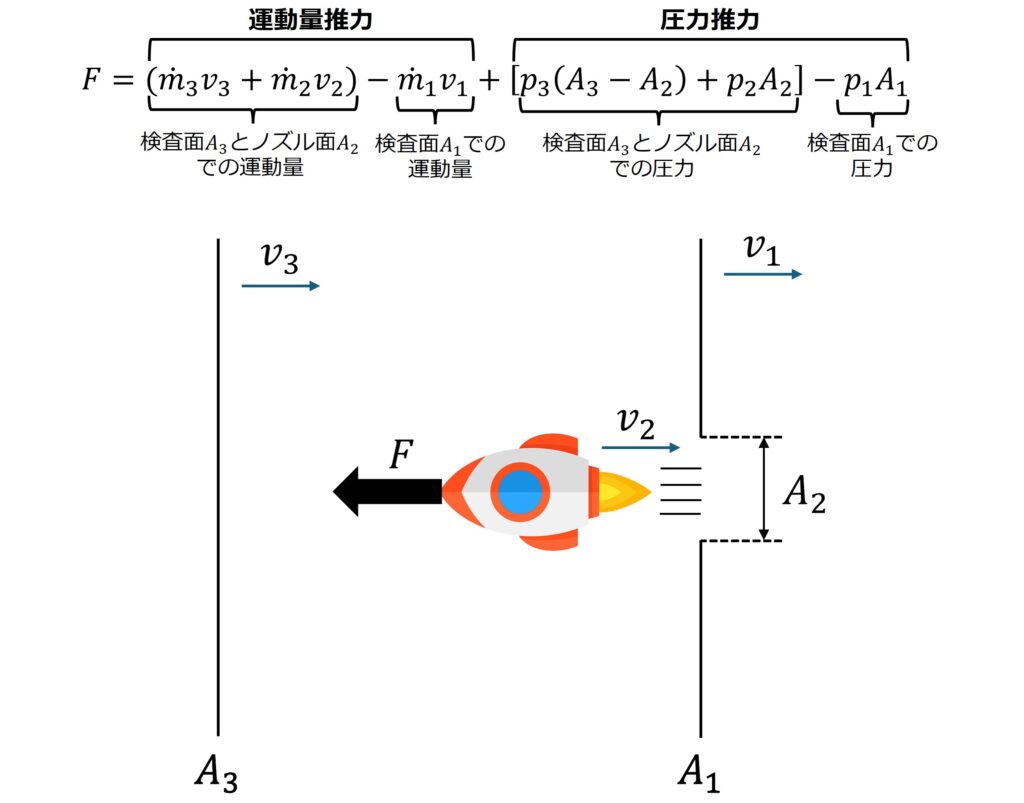
ロケットは定常流の中を移動しているので,大気の速度・圧力は一定です。よって,以下の式が成り立ちます。
$$\dot{m_{3}}v_{3}=\dot{m_{1}}v_{1} p_{3}A_{3}=p_{1}A_{1}\tag{3}$$
式(2)と式(3)よりロケットの推力\(F\)は以下のように計算できます。
$$F=\dot{m_{2}}\left[v_{2}+\frac{(p_{2}-p_{3})A_{2}}{\dot{m_{2}}}\right]\tag{4}$$
式(4)の大かっこの中身を有効排気速度\(c\)と呼びます。よって有効排気速度は式(5)で表すことができます。
$$c=v_{2}+\frac{(p_{2}-p_{3})A_{2}}{\dot{m_{2}}}\tag{5}$$
式(5)から有効排気速度とはロケットの速度\(v_{2}\)に圧力推力の要素を加えた値であることが分かります。
また,式(4)と式(5)より以下のように書くこともできます。
$$F=\dot{m_{2}}c\tag{6}$$
式(6)は運動方程式のような形になっていることが分かります。
(\(F=ma=m/t・ta=\dot{m}v\)より)
式(6)から,ロケットの推力を増大させるためには燃料の流量を増やすか有効排気速度を増やす必要があるということが分かります。
参考文献
- ロケットエンジン,中村佳朗 監修/鈴木弘一 著



コメント