比例航法

ミサイルが目標を補足したときはシーカを用いて，比例航法という制御則で目標を追尾します。

そこでミサイルの比例航法の概要と比例航法に関する式について解説を行います。

Point
式(1)の導出
式(2)の導出
式(3)の導出
参考文献

Point

比例航法とは，目視線角の変化に対してそれに対応するように自身の経路角を変化させる航法である。
比例航法は以下の3つの式で表される。なお，3つは全て同じ意味を持つ。

$$\dot{γ}=N\dot{σ}\tag{1}$$$$a_{m}=NV_{m}\dot{σ}\tag{2}$$$$n_{m}=N’V_{c}\dot{σ}\tag{3}$$

式(1)の導出

比例航法の概要はPointの式(1)の意味を理解すればよいです。よって式(1)の導出を行います。

まず，図1のような同一平面上での時刻$t$におけるミサイルM，目標T，会合点Iを考えます。

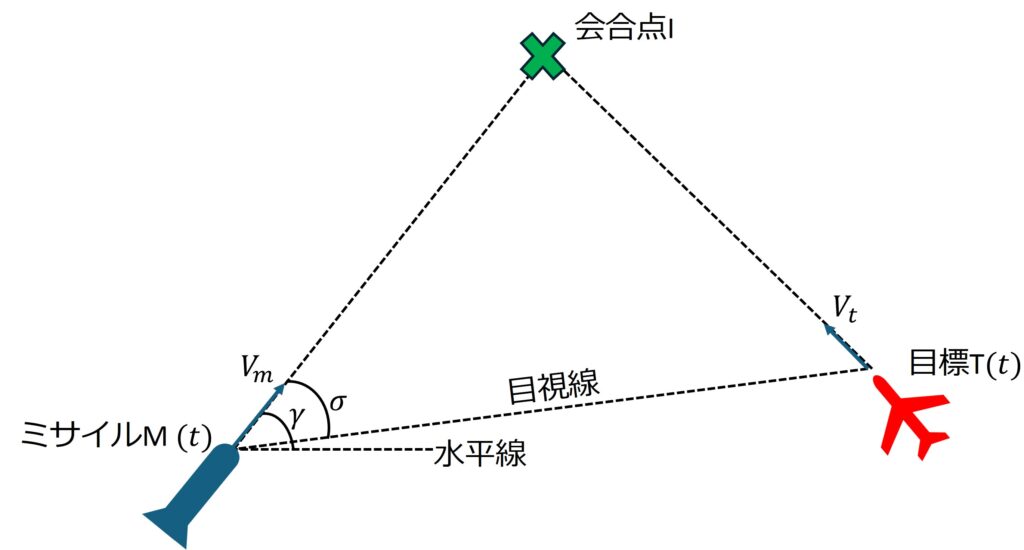
このような三角形を会合三角形と呼びます。

水平線とミサイルMの速度ベクトル$V_{m}$がなす角を経路角$γ$と呼び，目視線とミサイルMの速度ベクトル$V_{m}$がなす角を目視線角$σ$と呼びます。

ただし，目標TとミサイルMは以下の条件で飛しょうするものとします。

等速運動を行う
機体応答性については考慮しない（伝達関数は1）

また，目標Tが以下の2つのような飛しょうをしたときの状況を考えます。

等速直線運動
等速で旋回

まずは1つ目の目標Tが等速直線運動をした時の状況を考えます。
図1の会合三角形から$Δt$経過した，時刻$t+Δt$の状況を図2に示します。

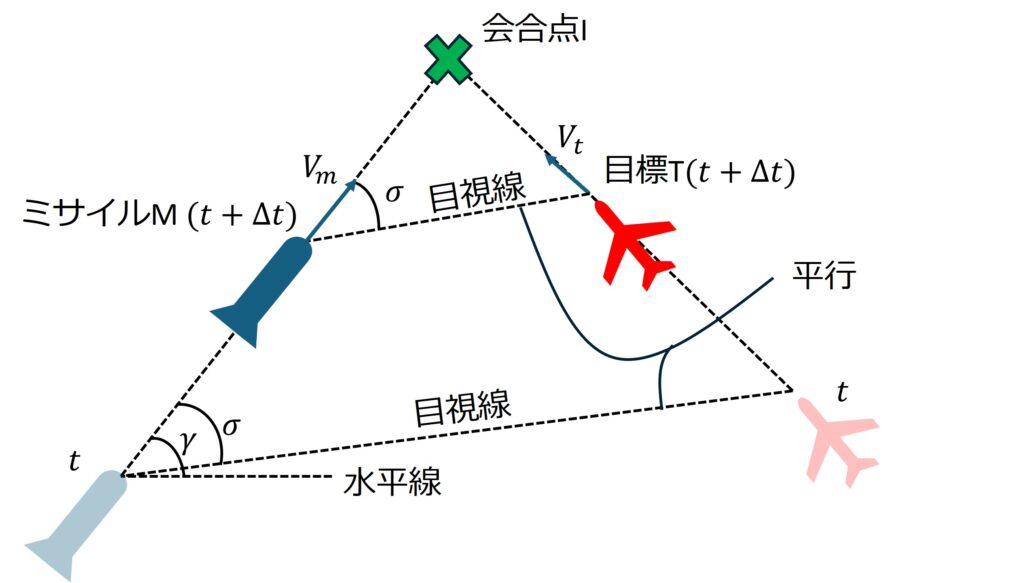
図2より，目標Tが等速直線運動をしているときは，目視線が平行，つまり目視線角$σ$が常に一定であるならば，ミサイルMもそのまま等速直線運動で飛しょうしていれば必ず点Iで会合することになります。

ここで重要なのは，目視線角が一定($\dot{σ}=0$)ならばミサイルMはそのまま等速直線運動($\dot{γ}=0$)で飛しょうさせるということです。

これは，式(1)に当てはめることができます。

式(1)より，$\dot{σ}=0$ならば$\dot{γ}=0$になります。

次に，目標Tが等速で旋回するとき($\dot{σ}\neq0$)を考えます。

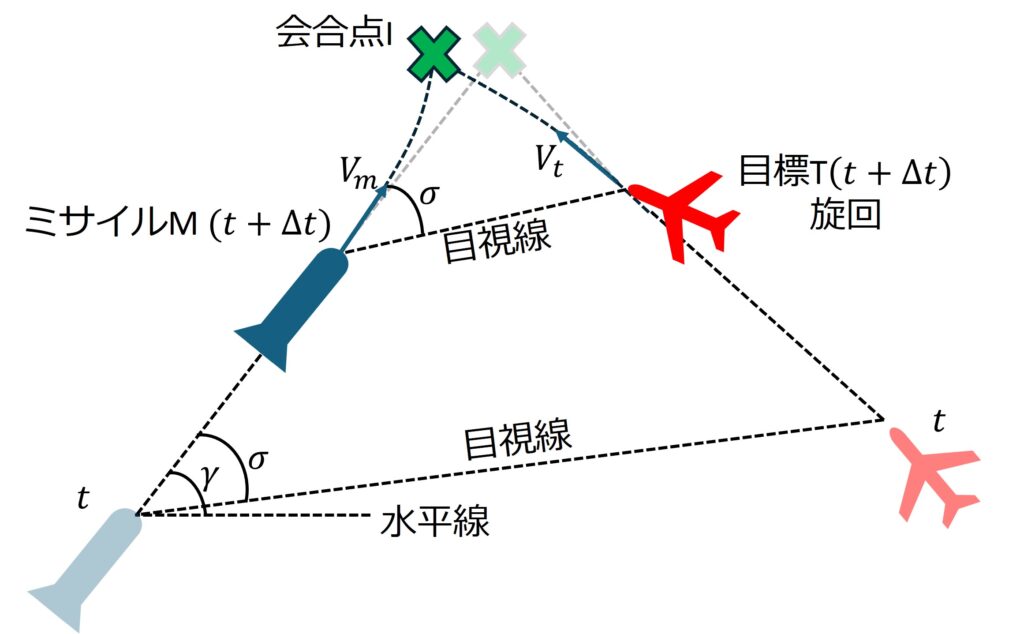
図3より，時刻$t+Δt$で目標Tが旋回する状況を考えます。

すると，会合点Iは移動し，目視線角に変化が生じます。

図2では目視線角が常に一定ならば目標Tに会合するという話をしました。

つまり，目視線角に変化が生じたならばその変化を抑えるようにミサイルMを旋回させてあげれば，移動した後の点Iで会合できるということです。

ではどのようにミサイルMを旋回させればよいのでしょうか。

それは目視線角の変化率$\dot{σ}$に比例させるようにミサイルMの経路角の変化率$\dot{γ}$を計算することで旋回させます。

よって，比例航法の式は以下のようになります。

$$\dot{γ}=N\dot{σ}\tag{1}$$

$N$を航法定数と呼び，目視線角$\dot{σ}$にゲインをかけることで経路角速度$\dot{γ}$を計算します。

よって，式(1)のように目視線角速度$\dot{σ}$に比例するように経路角速度$\dot{γ}$が計算される飛しょう方法が比例航法です。

式(2)の導出

比例航法とは目視線角速度$\dot{σ}$に比例するようにミサイルMの経路角速度$\dot{γ}$を制御することですが，実際ミサイルの経路角自体を制御するのは難しいです。

基本的にミサイルは加速度を算出することによって制御を行います。

そこで，式(1)の経路角速度の式から式(2)のような加速度の式に変形させます。

変形方法としては等速円運動の公式を用います。

「ミサイルMと目標Tは等速である」という状況を考えているため等速円運動の公式が使用できます。

等速円運動の式より速度ベクトルに直交する成分の加速度は以下の式で表されます。

$$a=vω$$

$ω$は角速度であり，比例航法の式(1)における，経路角速度$\dot{γ}$に該当します。

よって，$ω$に$\dot{γ}$を代入すると以下のようになります。

$$a_{m}=NV_{m}\dot{σ}\tag{2}$$

$a_{m}$はミサイルMの加速度を表し，目視線角速度$\dot{σ}$に対してミサイルMが出すべき加速度を計算することができます。

図4に，ミサイルMの加速度に関する図を示します。ミサイルMの加速度$a_{m}$は速度$V_{m}$に対して垂直方向に生じていることがわかります。

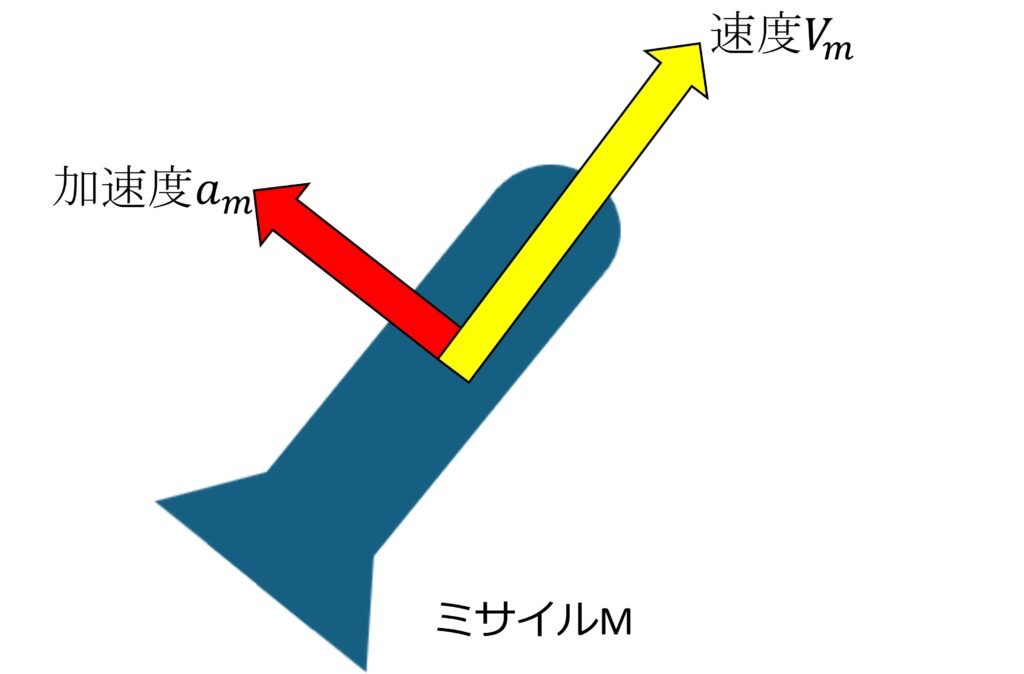
式(3)の導出

式(2)の導出ではミサイルMの加速度を比例航法によって算出することができることを確認しました。

式(2)で算出した加速度のうち目視線角の変化を抑えるために必要な加速度成分$n_{m}$は基準線に対して直交させた成分です。

$n_{m}$に関する図を以下に示します。

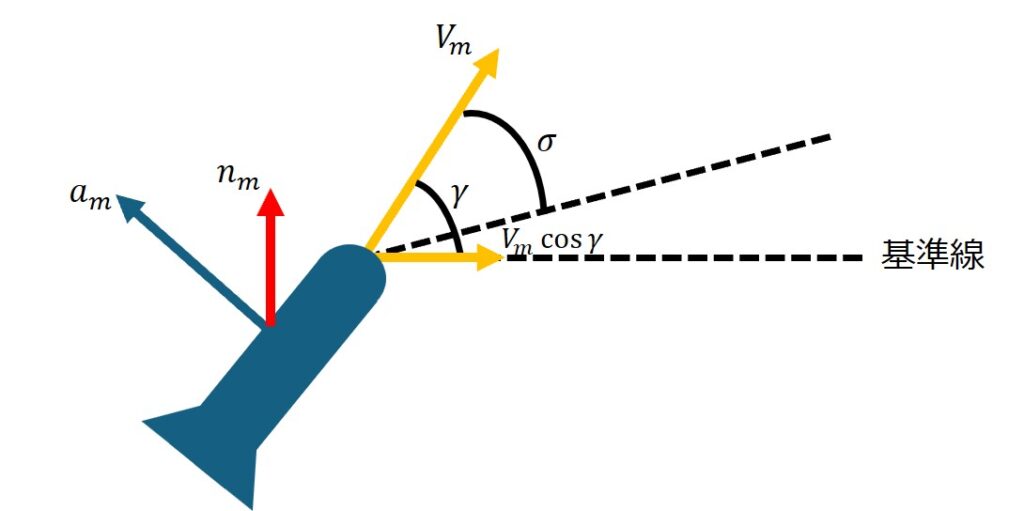
目視線角変化を抑えるための加速度$n_{m}$の式を表すと以下のようになります。

$$n_{m}=NV_{m}\cos{γ}\dot{σ}=N’V_{c}\dot{σ}\tag{3}$$

相対接近速度$V_{c}$は目視線方向の相対速度のことです。

$V_{m}\cos{γ}$と目視線方向の相対速度である相対接近速度$V_{c}$は異なるため相対接近速度を用いるときは有効航法定数$N’$を用います。

航法定数$N$と有効航法定数$N’$の関係は次のような式で表されます。

$$N’=\frac{NV_{m}\cos{γ}}{V_{c}}$$

ミサイルの設計において，ミサイルは自分自身の速度は知らなくても相対接近速度は知ることができます。

よって，ミサイルの設計において比例航法を使用するときは相対接近速度を使用する式(3)を用いることが多いです。

参考文献

・兵器と防衛技術のシリーズ③ ミサイル技術のすべて